Enginursday: Acoustic Noise Cancellation with Adaptive Signal Processing

Filter noise from your latest paranormal investigation field recordings, audio-capturing UAV or anything not related to either of those two things.

by LightningHawk October 13, 2016 2:29 pm UTC 13

• Engineering
• Programming

Favorited Favorite 2

An adaptive filter is designed to optimize non-linear, time-varying filters by updating its weight vector based on minimizing the error that is fed back into the system. Designing a filter that can adapt with time lends itself to useful characteristics such as training them to perform tasks without the designer having any prior knowledge of the system for which the filter is designed.

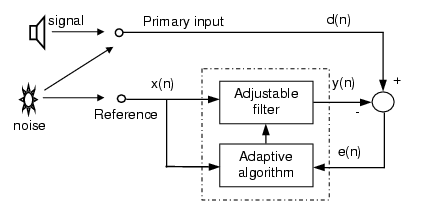
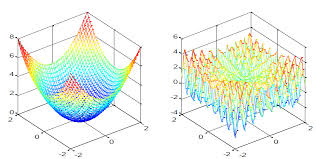
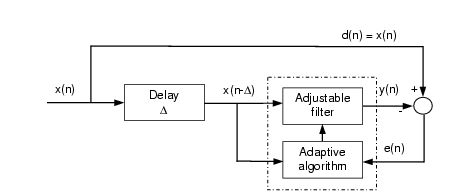
Adaptive interference canceling can be modeled as a feedback control system (diagram above) where d(n) is the desired output, y(n) is the output of the filter, and e(n) is the error or difference between the signals d(n) and y(n) at the summing junction. The error gets fed to the adaptive algorithm after each iteration. The primary input is the desired signal. The reference input contains the noise that is also contained in the primary input. The goal of the system is to get y(n), the output of the filter equal to the desired signal d(n) – the gradient at a point on the performance surface ideally equals zero. The performance surface is the plot of the expected value of the instantaneous squared error (error at each sample). The weight vector that can be calculated from the squared error is always a quadratic function. The LMS (Least-Mean Square) algorithm avoids the squaring by estimating the gradient without perturbation of the weight vector. From a single data point, the LMS algorithm can calculate the "steepest descent" along the performance surface by starting out with a wild guess and, in a way, will ask itself, "Which way to low-flat land?" Since each iteration is based on an estimate of the gradient, there is a fair amount of noise gained by the system, but it's attenuated with time and attenuated even further when the weight vector is kept from updating every iteration.

This is similar to how feedback in conference calls is eliminated. The feedback is the noise that can be heard on both ends but is definitely stronger on the producing side. The side with the "weaker" feedback is the desired output.

Below is an example project I created in Matlab (code provided in GitHub link below). I read a passage of a book over the sound of what could be a couple lawnmowers. The first half is the raw playback of the recording. Toward the end it is nearly impossible to distinguish my voice over the noise. The second audio recording that is played is the live, adaptively-filtered version of the original recording.

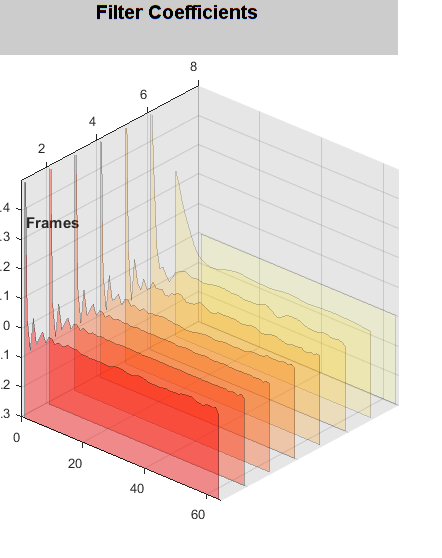
You can see from the waterfall plot above that once the algorithm has hammered out the range of the lowest possible error e(n), the noise becomes nearly non-existent. From the first 10 samples you can see the algorithm found the path of steepest descent. Then went up a bit and back down a bit until it figured out where the minimum error occurred. These filters usually start out with a high error and then settle around close to zero. In the last run you can see the error didn't start out so high and settled quicker than the previous runs.

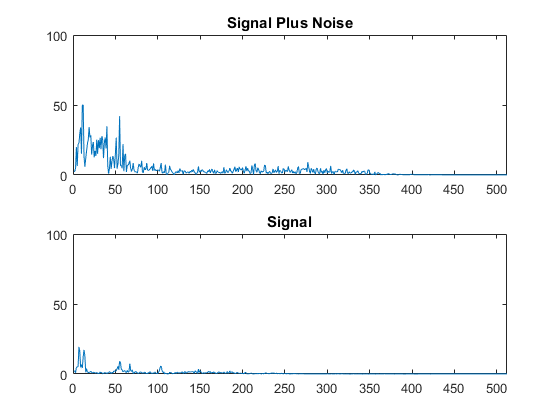
Here you are looking at the FFT of the desired output d(n) and the FFT of the error e(n). You can see how quickly the noise is canceled, and how well. The last 250-300 samples hardly change at all.

Here is the link to the GitHub page where I have pushed this program.

Food for thought: Given the control diagram below, the adaptive algorithm could be changed to become an adaptive predictor. With one input (could be something like the whole history of winning Lotto numbers) and a delay you are on your way to making your own prediction machine.

I may or may not already be working on this. For anyone interested in learning more and seeing the math, I highly recommend "Adaptive Signal Processing" by Bernard Widrow and Samual D. Stearns.